你不可不知数学的美到底在哪儿几种形式给人窒息版的享受
数学是美丽的,世间不是缺少美,而是缺少美的眼睛。数学绝不是枯燥无味的,而是一门充满美感,让人沉迷其中的学科。它的形式简单有序而又对称统一,它的内涵严谨简洁而又富含哲理性,它的和谐更是体现在数学的各个微小细节,它的曲折而坎坷的发展道路更像是孩子走向成熟的过程,让人感同身受而又无限向往。
数学可以使人更聪明,使人更美丽。得数学者得天下!数学美的不同表现形式有不同的形容:壮美、俊美、秀美、柔美、优美, 数学美也呈现多样性,我们分为:简洁美、对称美、和谐美和奇异美。

余弦定理的无字证明
一、简洁美
爱因斯坦说过:“美在本质上终究是简单性。”数学语言本身就是最简洁的文字,同时反映客观规律极其深刻,许多复杂的客观现象,总结为一定的规律时,往往呈现为十分简单的公式。
复杂的自然界中所有的一切,数学家都可以用自己简单的数字公式或语言高度抽象出来。他们以其简洁的形式,从一组简洁明了的公理、概念出发,进行精确计算、严谨推理,就可抽象推论出各种令人惊叹的定理或公式,使人们洞察到数学的内在和谐、严谨、逻辑和秩序性。计算机的代码简单得只有0和1,却可编写出无数深奥无比的程序软件;质数的定义:“只有1和它本身两个约数的数”中的一个“只”字一字值千金;“两点确定一条直线”中的“确定”高度概括了定义的严谨性。用简单的形式表达深遂的内涵,如同绘图时只用三种原色确可绘制出各种色彩缤纷的图画来,又如同音乐简谱中只凭借七个音符确谱写出了千万首动人的乐章……
如运算符号:

在数学美的各个属性中,首先要推崇的大概是简单性了。——(莫德尔 L.J.Mordell) 数学符号节省了人们的思维。——(莱布尼兹)。据我观察,“惰性”无论是在自然界,还是在人类的世界都受到我们的热烈追捧,只要能够偷懒,能够简洁,我们就绝不会去“多此一举”:光沿直线方向传播,这是因为它是最为便捷的距离;大雁迁徙时呈人字飞行,这是由于他们所受到得阻力最小……这些都向我们展示了万事万物的简洁与和谐。 宇宙万物都是如此,那数学更不用说了.

法国哲学家狄德说道:数学中所谓美的回答,是关于困难而繁杂的题目的简单回复。事实上,数学的简单是体现在简单的语言和求解方法简单。数学,不喜欢笨拙和复杂。数学之美,美在简洁的符号。数学符号的首要在于它 把自然和社会甚至于宇宙中的数学关联起来,去回答那些已知或未知的问题,去创造更新、更深的思维形式。如:
①表示数的符号,如0,1,2,…,8,9这类数字在学习了计数的方法后,我们将使用它们来代表不同的数字。
②括号,如(),[],{},等等;通过它,可以对代数符号与符号构成式子(或项),进行组织,使之能形成各种复杂的结构。括号在数学上,特别是代数公式语言的构成上起着十分重要的作用。
③语标符号,数学有一些语标符号。这是表示特定的数学对象的符号,其书写形态也 专门为此而“发明”的。大家最熟悉的数字0,1,2,…,9便是语标符号的例子,其他还有+、-、×、÷、 ,…,等等。
由此看来数学符号的作用还真不少,英国学者R.斯坎普开列了如下“菜单”——数学符号的十种功能:(1)传递;(2)记录知识;(3)形成新的概念;(4)简化复杂纷繁的分类系统;(5)解释;(6)使反思活动成为可能;(7)揭示结构;(8)使操作程序自动化;(9)信息的恢复与理解;(10)进行创造性的思考。
数学的简洁美还表现在形态上,即数学美的外部表现形态,是数学定理和数学公式(或表达式)的外在结构中呈现出来的美。形态美的主要特征,在于它的简单性。例如欧拉给出的公式:V-E+F=2,堪称“简单美”的典范。世间的多面体有多少没有人能说清楚。但它们的顶点数V、棱数E、面数F,都必须服从欧拉给出的公式,一个如此简单的公式,概括了无数种多面体的共同特性,令人惊叹不已。在数学中,像欧拉公式这样形式简洁、内容深刻、作用很大的定理还有许多。
比如:圆的周长公式:C=2πR 任意一个圆它的周长都满足这样的公式。英国科学家牛顿用F=ma概括了力、质量、加速度之间的定量关系;又如,德国科学家爱因斯坦用E=mc^2 揭示了自然界的质量和能量的转换关系;这里F=ma、E=mc^2就外在形式而论,都是非常简洁的,不失为数学形态美的范例。
数学中绝大部分公式都体现了“形式的简洁性,内容的丰富性”。正如伟大的希而伯特曾说过:“数学中每一步真正的进展都与更有力的工具和更简单的方法的发现密切联系着”。如笛卡尔坐标系的引入。对数符号的使用,复数单位的引入。微积分的出现都体现了数学外在形式更简洁,内容更深厚。

著名的皮亚诺公式只用了三个不加定义的原始概念和五个不加证明的公理,显示了逻辑上的简洁。由此产生的自然数理论是现代数学基础研究的起点,这三个原始概念是“自然数”,“1”,“后继(数)”;五个公理是:
公理一:1是自然数,
公理二:任何自然数的后继也是自然数,
公理三:没有两个自然数有相同的后继,
公理四:1不是任何自然数的后继,
公理五:若一个有自然数组成的集合S含有1,且当S含有任一个自然数时,也一定含有它的后继,则S就含有全体自然数。
世事再纷繁,
加减乘除算尽,
宇宙虽广大,
点线面体包完。
这首诗,用字不多,却到位地概括出了数学的简洁明了,微言大义。数学和诗歌一样有着独特的简洁美。 诗歌的简洁,众所周知——着寥寥几字,却为读者创造出了广阔的想象空间,这大概正是诗歌的魅力所在。
美国著名心理学家L布隆菲尔德L•Bloonfield说“数学是语言所能达到的最高境界。”如果说诗歌的简洁是写意的,是欲言还休的,是中国水墨画中的留白,那么数学语言的微言大义,则是写实的,是简洁精确、抽象规范的,是严谨的科学态度的体现。数学的简洁,不仅使人们更快、更准确地把握理论的精髓,促进自身学科的发展,也使数学学科具有了很强的通用性。

二、对称美
所谓对称性,既指组成某一事物或对象的两个部分的对等性,从古希腊的时代起,对称性就被认为是数学美的一个基本内容。毕达哥拉斯就曾说过:“一切平面图形中最美的是圆,在一切立体图形中最美的是球形。”这正是基于这两种形体在各个方向上都是对称的。
“对称”在数学上的表现则是普遍的,几何上平面的情形有直线对称(轴对称)和点对称(中心对称),空间的情形除了直线和点对称外,还有平面对称。正偶边形既是中心对称图形又是轴对称, 正奇边形不是中心对称图形但是轴对称。比如正方形既是轴对称图形(以过对边中点的直线为轴),以是中心对称图形(对角线的交点为对称中心),圆也是。

还有一些优美的曲线是数学形象美与和谐的结合产物。如得之于自然界的四叶玫瑰线、对数螺旋线,还有那久负盛名的莫比乌斯曲线。莫比乌斯曲线的和谐美不仅局限于它的外观,它还体现在“在二维空间里构造一维空间”的合二为一的高度内敛的和谐美。把一个长纸条,一端扭转后再与另一端粘贴起来,那么当一只蚂蚁从纸条任意一点沿着一面出发,却可途经纸条的两面所有路线之后而又回到原点。这一神奇的“合二为一”构造术映射出了一个伟大的数学与交际结合的哲理——化敌为友,敌友一家亲并非妄然。
数的外在美,是一种没有经过加工的自然美,毕达哥拉斯将自然界和数统一在一起,他说:凡物皆数。伽利略说:自然这本书是用数学语言写成的。我说:我的人生是数的人生。
毕达哥拉斯有句名言:“一切立体图形中最美的是球形,一切平面图形中最美的是圆形。”而圆和球形正是几何中对称美的杰出体现。圆是关于圆心对称的,也是关于过圆心的任意一条直线对称。球形既是点对称,又是线对称,还是面对称。正是由于几何图形中有这些点对称、线对称、面对称,才够成了美丽的图案,精美的建筑,巧夺天工的生活世界,也才给我们带来丰富的自然美和多彩的生活美。

牛顿动态函数
三、统一美
数学起源于哲学,哲学中的对立统一规律反映在数学上就是其统一性。统一是简单的基础,简单是数学的魅力。用统一的眼光看数学,则动与静是统一的,数与式是统一的,运算与映射是统一的,二维与三维是统一的。
例如,引入负数,有了相反数的概念之后,有理数的加法和减法得到统一,它们可以统一为代数和的形式。有了倒数的概念,除以一个不等于零的数等于乘上它的倒数,于是乘法与除法得到了统一。例如平面几何中的相交弦定理、割线定理、切割线定理和切线长定理均可统一到圆幂定理之中。在体积计算中有所谓的“万能计算公式”,它能统一地应用于棱(圆)柱、棱(圆)锥及棱(圆)台的体积计算
统一美反映的是审美对象在形式或内容上的某种共同性、关联性或一致性,它能给人一种整体和谐的美感。数学对象的统一性通常表现为数学概念、规律、方法的统一,数学理论的统一,数学和科学的统一。

神奇的数学之心
数学概念、规律、方法的统一。一切客观事物都是相互联系的,因而,作为反映客观事物的数学概念、数学定理、数学公式、数学法则也是互相联系的,在一定条件下可处于一个统一体之中。例如,运算、变换、函数分别是代数、几何、分析这三个数学分支中的重要概念,在集合论中,便可统一于映射的概念。又如代数中的算术平均——几何平均定理、加权平均定理、幂平均定理、加权幂平均定理等著名不等式,都可以统一于一元凹、凸函数的琴森不等式。
在数学方法上,同样渗透着统一性的美。例如,从结构上分析,解析法、三角法、复数法、向量法和图解等具体方法,都可以统一于数形结合法。数学中的公理化方法,使零散的数学知识用逻辑的链条串联起来,形成完整的知识体系,在本质上体现了部分和整体之间的和谐统一。
数学理论的统一。在数学发现的历史过程中,一直存在着分化和整体化两种趋势。数学理论的统一性主要表现在它的整体性趋势。欧几里德的《几何原本》,把一些空间性质简化为点、线、面、体几个抽象概念和五条公设及五条公理,并由此导致出一套雅致的演绎理论体系,显示出高度的统一性。布尔基学派的《数学原本》,用结构的思想和语言来重新整理各个数学分支,在本质上揭示数学的内在联系,使之成为一个有机整体,在数学的高度统一性上给人一美的启迪。
微分和积分最先是当作两种数学的运算、两类的数学问题来分别以研究。但是当牛顿与莱布尼茨独立地将微分和积分真正沟通,用微积分基本定理使得这两种数学的运算统一起来,正确清楚地找到了两种运算的内在的联系:微分和积分是互逆的两种运算,微积分学才真正的建立起来。
建立射影几何的数学统一的典型结果。相比与欧氏几何,射影几何的一个重要特征是点与直线的对称统一。由于引进的无穷远点,点和线在射影几何中的地位是完全对称的,这也促使了射影几何的建立。

笛卡尔开创了几何形式与代数形式在数学内部横向统一,将坐标系引入几何,使曲线与方程得以互化,按照自己的方案统一了欧氏几何。
数学和科学的统一。数学和科学的相互渗透,导致了科学数学化。正如马克思所说的,一门科学只有当它成功的运用数学时,才算达到了真正完善的地步。力学的数学化使牛顿建立了经典力学体系。科学的数学化使物理学与数学趋于统一。建立在相对论和量子论两大基础理论上的物理学,其各个分支都离不开数学方法的应用,它们的理论表述也采用了数学的形式。化学的数学化加速了化学这门实验性很强的学科向理论科学和精确科学过渡。生物数学化使生物学日益摆脱对生命过程进行现象描述的阶段,从定性研究转向定量研究,这个数学化的方向,必将同物理学、化学的数学化方向一样,把人类对生命世界的认识提高到一个崭新的水平。不仅自然科学普遍数学化了,而且数学方法也进入了经济学、法学、人口学、人种学、史学、考古学、语言学、文学等社会科学领域,日益显示出它的效用。数学进入经济学领域最大的成就是本世纪出现的计量经济学。数学进入语言学领域,使语言学研究经历了统计语言学、代数语言学和算法语言学三个阶段。数学向文学的渗透,发现了数学的抽象推理和符号运算同文学的形象思维之间有着奇妙的联系。

四、奇异美
数学家庞加莱说:“数学的优美感不过就是问题的解答适合我们心灵需要而产生的一种满足。”数学思想方法、数学模型化方法是一道道绚丽多姿的耀眼的光芒,它们独特的奇异美,精巧绝伦,令人赏心悦目。充分利用这种不可抗拒的奇异美的魅力,可以培养学生的求异意识,从而逐步培养起创新意识以至创造性思维的能力。稀罕、出乎意料但却引人入胜!
奇异性是数学内涵美的又一基本内容。它是指所得的结果新颖奇特,出人意料。七巧板拼图是小学初中数学课常采用的内容。用七块板可以拼成一个最简单的正方形,也可以拼出千变万化的复杂图案:如人形、鸟兽、花草、房屋等。通过七巧板拼图练习,学生感到图案之多,出人意料;图形之美,妙趣横生。

1、分数的奇异性

2、费马猜想
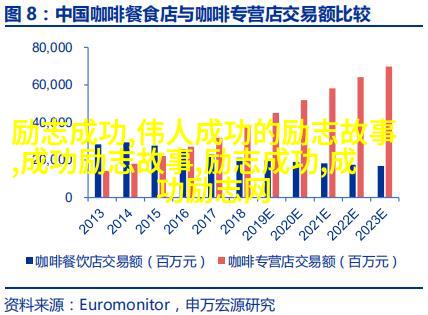
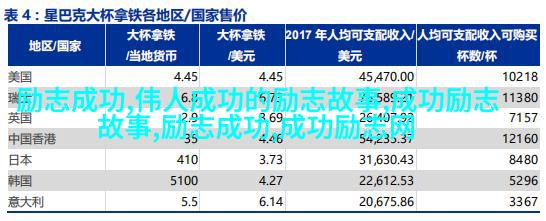
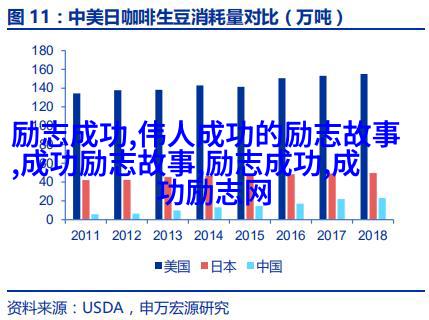
18世纪最伟大的数学家欧拉(Euler)证明了n=3,4时费马定理成立;后来,有人证明当n<10^5是定理成立。20世纪80年代以来,取得了突破性的进展。1995年英国数学家Andrew Wiles(安德鲁˙怀尔斯,
普林斯顿大学教授)的108页论文解决了费马定理。他1996年获wolf奖,1998年获Fielz奖。(伍尔佛基金会奖(Wolf Foundation Prizes) 宗旨:成立于1978年,为前古巴派驻以色列外交家、发明家、慈善家Dr. Ricardo Wolf发起,为奖励杰出科学家、艺术家对人类的贡献,不论国籍、种族、性别、信念。 奖赏以下列领域为主:农业、化学、)...

数学美育是数学教育中的一朵艳丽多姿的奇葩,是数学教育中一道辉煌灿烂的曙光。它对培养非智力因素,提高学习兴趣,以趣激学,促使学生良好的数学素质的逐步形成,有着非常重要的作用。教学中是否善于适时地挖掘美育,让学生受到数学美的艺术熏陶,将是数学教学成功与否的关键。
布朗树
数是美的元素,数学是美丽的学科!真正的数学家把对数学的研究、追求当作有着艺术享受的快乐。“美好事物总是一种永久享受!”世界上没有什么力量能把数学家从他的“美人”身边拉走,他们是世界上最忠贞的情人,他们会一生许多次堕入爱河,每一次的对象都是同一个人。



